Data Whitening¶
A whitening transformation is a decorrelation transformation that transforms a set of random variables into a set of new random variables with identity covariance (uncorrelated with unit variances).
In particular, suppose a random vector has covariance 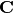 , then a whitening transform
, then a whitening transform 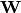 is one that satisfy:
is one that satisfy:
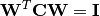
Note that 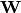 is generally not unique. In particular, if
is generally not unique. In particular, if 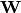 is a whitening transform, so is any of its rotation
is a whitening transform, so is any of its rotation 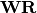 with
with 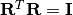 .
.
Whitening¶
The package uses Whitening defined below to represent a whitening transform:
immutable Whitening{T<:FloatingPoint}
mean::Vector{T} # mean vector (can be empty to indicate zero mean), of length d
W::Matrix{T} # the transform coefficient matrix, of size (d, d)
end
An instance of Whitening can be constructed by Whitening(mean, W).
There are several functions to access the properties of a whitening transform f:
-
indim(f)¶ Get the input dimension, i.e
d.
-
outdim(f)¶ Get the out dimension, i.e
d.
-
mean(f)¶ Get the mean vector.
Note: if
f.meanis empty, this function returns a zero vector of lengthd.
-
transform(f, x)¶ Apply the whitening transform to a vector or a matrix with samples in columns, as
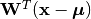 .
.
Data Analysis¶
Given a dataset, one can use the fit method to estimate a whitening transform.
-
fit(Whitening, X; ...)¶ Estimate a whitening transform from the data given in
X. Here,Xshould be a matrix, whose columns give the samples.This function returns an instance of
Whitening.Keyword Arguments:
name description default regcoef The regularization coefficient. The covariance will be regularized as follows when
regcoefis positive:C + (eigmax(C) * regcoef) * eye(d)zero(T)mean The mean vector, which can be either of:
0: the input data has already been centralizednothing: this function will compute the mean- a pre-computed mean vector
nothingNote: This function internally relies on
cov_whitento derive the transformationW. The functioncov_whitenitself is also a useful function.
-
cov_whitening(C)¶ Derive the whitening transform coefficient matrix
Wgiven the covariance matrixC. Here,Ccan be either a square matrix, or an instance ofCholesky.Internally, this function solves the whitening transform using Cholesky factorization. The rationale is as follows: let
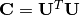 and
and 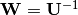 , then
, then 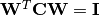 .
.Note: The return matrix
Wis an upper triangular matrix.
-
cov_whitening(C, regcoef) Derive a whitening transform based on a regularized covariance, as
C + (eigmax(C) * regcoef) * eye(d).
In addition, the package also provides cov_whiten!, in which the input matrix C will be overwritten during computation. This can be more efficient when C is no longer used.
-
invsqrtm(C)¶ Compute
inv(sqrtm(C))through symmetric eigenvalue decomposition.