Independent Component Analysis¶

Independent Component Analysis (ICA) is a computational technique for separating a multivariate signal into additive subcomponents, with the assumption that the subcomponents are non-Gaussian and independent from each other.

There are multiple algorithms for ICA. Currently, this package implements the Fast ICA algorithm.

ICA¶

The package uses a type ICA, defined below, to represent an ICA model:

mutable struct ICA{T<:Real}
    mean::Vector{T}   # mean vector, of length m (or empty to indicate zero mean)
    W::Matrix{T}      # component coefficient matrix, of size (m, k)
end

Note: Each column of W here corresponds to an independent component.

Several methods are provided to work with ICA. Let M be an instance of ICA:

indim(M)¶: Get the input dimension, i.e the number of observed mixtures.

outdim(M)¶: Get the output dimension, i.e the number of independent components.

mean(M)¶

Get the mean vector.

Note: if M.mean is empty, this function returns a zero vector of length indim(M).

transform(M, x)¶: Transform x to the output space to extract independent components, as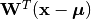 $\mathbf{W}^T (\mathbf{x} - \boldsymbol{\mu})$ .

Data Analysis¶

One can use fit to perform ICA over a given data set.

fit(ICA, X, k; ...)¶

Perform ICA over the data set given in X.

Parameters:

X – The data matrix, of size (m, n). Each row corresponds to a mixed signal, while each column corresponds to an observation (e.g all signal value at a particular time step).
k – The number of independent components to recover.

Returns:

The resultant ICA model, an instance of type ICA.

Note: If do_whiten is true, the return W satisfies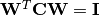 $\mathbf{W}^T \mathbf{C} \mathbf{W} = \mathbf{I}$ , otherwise W is orthonormal, i.e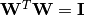 $\mathbf{W}^T \mathbf{W} = \mathbf{I}$

Keyword Arguments:

name	description	default
alg	The choice of algorithm (must be `:fastica`)	`:fastica`
fun	The approx neg-entropy functor. It can be obtained using the function `icagfun`. Now, it accepts the following values: `icagfun(:tanh)` `icagfun(:tanh, a)` `icagfun(:gaus)`	`icagfun(:tanh)`
do_whiten	Whether to perform pre-whitening	`true`
maxiter	Maximum number of iterations	`100`
tol	Tolerable change of `W` at convergence	`1.0e-6`
mean	The mean vector, which can be either of: `0`: the input data has already been centralized `nothing`: this function will compute the mean a pre-computed mean vector	`nothing`
winit	Initial guess of `W`, which should be either of: empty matrix: the function will perform random initialization a matrix of size `(k, k)` (when `do_whiten`) a matrix of size `(m, k)` (when `!do_whiten`)	`zeros(0,0)`
verbose	Whether to display iteration information	`false`

Core Algorithms¶

The package also exports functions of the core algorithms. Sometimes, it can be more efficient to directly invoke them instead of going through the fit interface.

fastica!(W, X, fun, maxiter, tol, verbose)

Invoke the Fast ICA algorithm.

Parameters:

W – The initial un-mixing matrix, of size (m, k). The function updates this matrix inplace.
X – The data matrix, of size (m, n). This matrix is input only, and won’t be modified.
fun – The approximate neg-entropy functor, which can be obtained using icagfun (see above).
maxiter – Maximum number of iterations.
tol – Tolerable change of W at convergence.
verbose – Whether to display iteration information.

Returns:

The updated W.

Note: The number of components is inferred from W as size(W, 2).