Principal Component Analysis¶
Principal Component Analysis (PCA) derives an orthogonal projection to convert a given set of observations to linearly uncorrelated variables, called principal components.
This package defines a PCA type to represent a PCA model, and provides a set of methods to access the properties.
Properties¶
Let M be an instance of PCA, d be the dimension of observations, and p be the output dimension (i.e the dimension of the principal subspace)
-
indim(M)¶ Get the input dimension
d, i.e the dimension of the observation space.
-
outdim(M)¶ Get the output dimension
p, i.e the dimension of the principal subspace.
-
mean(M)¶ Get the mean vector (of length
d).
-
projection(M)¶ Get the projection matrix (of size
(d, p)). Each column of the projection matrix corresponds to a principal component.The principal components are arranged in descending order of the corresponding variances.
-
principalvars(M)¶ The variances of principal components.
-
tprincipalvar(M)¶ The total variance of principal components, which is equal to
sum(principalvars(M)).
-
tresidualvar(M)¶ The total residual variance.
-
tvar(M)¶ The total observation variance, which is equal to
tprincipalvar(M) + tresidualvar(M).
-
principalratio(M)¶ The ratio of variance preserved in the principal subspace, which is equal to
tprincipalvar(M) / tvar(M).
Transformation and Construction¶
Given a PCA model M, one can use it to transform observations into principal components, as
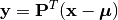
or use it to reconstruct (approximately) the observations from principal components, as
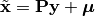
Here, 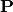 is the projection matrix.
is the projection matrix.
The package provides methods to do so:
-
transform(M, x)¶ Transform observations
xinto principal components.Here,
xcan be either a vector of lengthdor a matrix where each column is an observation.
-
reconstruct(M, y)¶ Approximately reconstruct observations from the principal components given in
y.Here,
ycan be either a vector of lengthpor a matrix where each column gives the principal components for an observation.
Data Analysis¶
One can use the fit method to perform PCA over a given dataset.
-
fit(PCA, X; ...)¶ Perform PCA over the data given in a matrix
X. Each column ofXis an observation.This method returns an instance of
PCA.Keyword arguments:
Let
(d, n) = size(X)be respectively the input dimension and the number of observations:name description default method The choice of methods:
:auto: use:covwhend < nor:svdotherwise:cov: based on covariance matrix:svd: based on SVD of the input data
:automaxoutdim Maximum output dimension. min(d, n)pratio The ratio of variances preserved in the principal subspace. 0.99mean The mean vector, which can be either of:
0: the input data has already been centralizednothing: this function will compute the mean- a pre-computed mean vector
nothingNotes:
- The output dimension
pdepends on bothmaxoutdimandpratio, as follows. Suppose the firstkprincipal components preserve at leastpratioof the total variance, while the firstk-1preserves less thanpratio, then the actual output dimension will bemin(k, maxoutdim). - This function calls
pcacovorpcasvdinternally, depending on the choice of method.
Example:
using MultivariateStats
# suppose Xtr and Xte are training and testing data matrix,
# with each observation in a column
# train a PCA model
M = fit(PCA, Xtr; maxoutdim=100)
# apply PCA model to testing set
Yte = transform(M, Xte)
# reconstruct testing observations (approximately)
Xr = reconstruct(M, Yte)
Example with iris dataset and plotting:
using MultivariateStats, RDatasets, Plots
plotly() # using plotly for 3D-interacive graphing
# load iris dataset
iris = dataset("datasets", "iris")
# split half to training set
Xtr = convert(Array,DataArray(iris[1:2:end,1:4]))'
Xtr_labels = convert(Array,DataArray(iris[1:2:end,5]))
# split other half to testing set
Xte = convert(Array,DataArray(iris[2:2:end,1:4]))'
Xte_labels = convert(Array,DataArray(iris[2:2:end,5]))
# suppose Xtr and Xte are training and testing data matrix,
# with each observation in a column
# train a PCA model, allowing up to 3 dimensions
M = fit(PCA, Xtr; maxoutdim=3)
# apply PCA model to testing set
Yte = transform(M, Xte)
# reconstruct testing observations (approximately)
Xr = reconstruct(M, Yte)
# group results by testing set labels for color coding
setosa = Yte[:,Xte_labels.=="setosa"]
versicolor = Yte[:,Xte_labels.=="versicolor"]
virginica = Yte[:,Xte_labels.=="virginica"]
# visualize first 3 principal components in 3D interacive plot
p = scatter(setosa[1,:],setosa[2,:],setosa[3,:],marker=:circle,linewidth=0)
scatter!(versicolor[1,:],versicolor[2,:],versicolor[3,:],marker=:circle,linewidth=0)
scatter!(virginica[1,:],virginica[2,:],virginica[3,:],marker=:circle,linewidth=0)
plot!(p,xlabel="PC1",ylabel="PC2",zlabel="PC3")
Core Algorithms¶
Two algorithms are implemented in this package: pcacov and pcastd.
-
pcacov(C, mean; ...)¶ Compute PCA based on eigenvalue decomposition of a given covariance matrix
C.Parameters: - C – The covariance matrix.
- mean – The mean vector of original samples, which can be a vector of length
d, or an empty vectorFloat64[]indicating a zero mean.
Returns: The resultant PCA model.
Note: This function accepts two keyword arguments:
maxoutdimandpratio.
-
pcasvd(Z, mean, tw; ...)¶ Compute PCA based on singular value decomposition of a centralized sample matrix
Z.Parameters: - Z – provides centralized samples.
- mean – The mean vector of the original samples, which can be a vector of length
d, or an empty vectorFloat64[]indicating a zero mean.
Returns: The resultant PCA model.
Note: This function accepts two keyword arguments:
maxoutdimandpratio.