Linear Discriminant Analysis¶
Linear Discriminant Analysis are statistical analysis methods to find a linear combination of features for separating observations in two classes.
Note: Please refer to Multi-class Linear Discriminant Analysis for methods that can discriminate between multiple classes.
Overview of LDA¶
Suppose the samples in the positive and negative classes respectively with means: 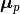 and
and 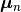 , and covariances
, and covariances 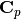 and
and 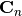 . Then based on Fisher’s Linear Discriminant Criteria, the optimal projection direction can be expressed as:
. Then based on Fisher’s Linear Discriminant Criteria, the optimal projection direction can be expressed as:
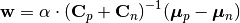
Here α is an arbitrary non-negative coefficient.
Linear Discriminant¶
A linear discriminant functional can be written as
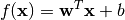
Here, w is the coefficient vector, and b is the bias constant.
This package uses the LinearDiscriminant type, defined as below, to capture a linear discriminant functional:
immutable LinearDiscriminant <: Discriminant
w::Vector{Float64}
b::Float64
end
This type comes with several methods. Let f be an instance of LinearDiscriminant
-
length(f)¶ Get the length of the coefficient vector.
-
evaluate(f, x)¶ Evaluate the linear discriminant value, i.e
w'x + b.When
xis a vector, it returns a real value; whenxis a matrix with samples in columns, it returns a vector of lengthsize(x, 2).
-
predict(f, x)¶ Make prediction. It returns
trueiffevaluate(f, x)is positive.
Data Analysis¶
The package provides several functions to perform Linear Discriminant Analysis.
-
ldacov(Cp, Cn, μp, μn)¶ Performs LDA given covariances and mean vectors.
Parameters: - Cp – The covariance matrix of the positive class.
- Cn – The covariance matrix of the negative class.
- μp – The mean vector of the positive class.
- μn – The mean vector of the negative class.
Returns: The resultant linear discriminant functional of type
LinearDiscriminant.Note: The coefficient vector is scaled such that
w'μp + b = 1andw'μn + b = -1.
-
ldacov(C, μp, μn) Performs LDA given a covariance matrix and both mean vectors.
Parameters: - C – The pooled covariane matrix (i.e
(Cp + Cn)/2) - μp – The mean vector of the positive class.
- μn – The mean vector of the negative class.
Returns: The resultant linear discriminant functional of type
LinearDiscriminant.Note: The coefficient vector is scaled such that
w'μp + b = 1andw'μn + b = -1.- C – The pooled covariane matrix (i.e
-
fit(LinearDiscriminant, Xp, Xn)¶ Performs LDA given both positive and negative samples.
Parameters: - Xp – The sample matrix of the positive class.
- Xn – The sample matrix of the negative class.
Returns: The resultant linear discriminant functional of type
LinearDiscriminant.