Multi-class Linear Discriminant Analysis¶

Multi-class LDA is a generalization of standard two-class LDA that can handle arbitrary number of classes.

Overview¶

Multi-class LDA is based on the analysis of two scatter matrices: within-class scatter matrix and between-class scatter matrix.

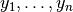Given a set of samples $\mathbf{x}_1, \ldots, \mathbf{x}_n$ , and their class labels $y_1, \ldots, y_n$ :

The within-class scatter matrix is defined as:

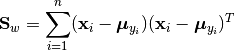
$\mathbf{S}_w = \sum_{i=1}^n (\mathbf{x}_i - \boldsymbol{\mu}_{y_i}) (\mathbf{x}_i - \boldsymbol{\mu}_{y_i})^T$

Here, 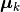$\boldsymbol{\mu}_k$ is the sample mean of the k-th class.

The between-class scatter matrix is defined as:

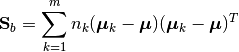
$\mathbf{S}_b = \sum_{k=1}^m n_k (\boldsymbol{\mu}_k - \boldsymbol{\mu}) (\boldsymbol{\mu}_k - \boldsymbol{\mu})^T$

Here, m is the number of classes, 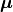$\boldsymbol{\mu}$ is the overall sample mean, and 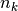$n_k$ is the number of samples in the k-th class.

Then, multi-class LDA can be formulated as an optimization problem to find a set of linear combinations (with coefficients 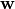$\mathbf{w}$ ) that maximizes the ratio of the between-class scattering to the within-class scattering, as

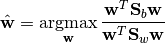
$\hat{\mathbf{w}} = \mathop{\mathrm{argmax}}_{\mathbf{w}} \frac{\mathbf{w}^T \mathbf{S}_b \mathbf{w}}{\mathbf{w}^T \mathbf{S}_w \mathbf{w}}$

The solution is given by the following generalized eigenvalue problem:

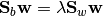
(1) $\mathbf{S}_b \mathbf{w} = \lambda \mathbf{S}_w \mathbf{w}$

Generally, at most m - 1 generalized eigenvectors are useful to discriminate between m classes.

When the dimensionality is high, it may not be feasible to construct the scatter matrices explicitly. In such cases, see SubspaceLDA below.

Normalization by number of observations¶

An alternative definition of the within- and between-class scatter matrices normalizes for the number of observations in each group:

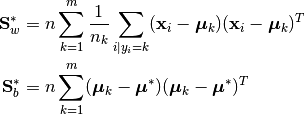
$\mathbf{S}_w^* &= n \sum_{k=1}^m \frac{1}{n_k} \sum_{i \mid y_i=k} (\mathbf{x}_i - \boldsymbol{\mu}_{k}) (\mathbf{x}_i - \boldsymbol{\mu}_{k})^T \mathbf{S}_b^* &= n \sum_{k=1}^m (\boldsymbol{\mu}_k - \boldsymbol{\mu}^*) (\boldsymbol{\mu}_k - \boldsymbol{\mu}^*)^T$

where

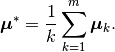
$\boldsymbol{\mu}^* = \frac{1}{k} \sum_{k=1}^m \boldsymbol{\mu}_k.$

This definition can sometimes be more useful when looking for directions which discriminate among clusters containing widely-varying numbers of observations.

Multi-class LDA¶

The package defines a MulticlassLDA type to represent a multi-class LDA model, as:

type MulticlassLDA
    proj::Matrix{Float64}
    pmeans::Matrix{Float64}
    stats::MulticlassLDAStats
end

Here, proj is the projection matrix, pmeans is the projected means of all classes, stats is an instance of MulticlassLDAStats that captures all statistics computed to train the model (which we will discuss later).

Several methods are provided to access properties of the LDA model. Let M be an instance of MulticlassLDA:

indim(M)¶: Get the input dimension (i.e the dimension of the observation space).

outdim(M)¶: Get the output dimension (i.e the dimension of the transformed features).

projection(M)¶: Get the projection matrix (of size d x p).

mean(M)¶: Get the overall sample mean vector (of length d).

classmeans(M)¶: Get the matrix comprised of class-specific means as columns (of size (d, m)).

classweights(M)¶: Get the weights of individual classes (a vector of length m). If the samples are not weighted, the weight equals the number of samples of each class.

withinclass_scatter(M)¶: Get the within-class scatter matrix (of size (d, d)).

betweenclass_scatter(M)¶: Get the between-class scatter matrix (of size (d, d)).

transform(M, x)¶

Transform input sample(s) in x to the output space. Here, x can be either a sample vector or a matrix comprised of samples in columns.

In the pratice of classification, one can transform testing samples using this transform method, and compare them with M.pmeans.

Data Analysis¶

One can use fit to perform multi-class LDA over a set of data:

fit(MulticlassLDA, nc, X, y; ...)¶

Perform multi-class LDA over a given data set.

Parameters:	nc – the number of classes X – the matrix of input samples, of size `(d, n)`. Each column in `X` is an observation. y – the vector of class labels, of length `n`. Each element of `y` must be an integer between `1` and `nc`.
Returns:	The resultant multi-class LDA model, of type `MulticlassLDA`.

Keyword arguments:

name description default

method

The choice of methods:

:gevd: based on generalized eigenvalue decomposition
:whiten: first derive a whitening transform from Sw and then solve the problem based on eigenvalue decomposition of the whiten Sb.

:gevd

outdim The output dimension, i.e dimension of the transformed space min(d, nc-1)

regcoef The regularization coefficient. A positive value regcoef * eigmax(Sw) is added to the diagonal of Sw to improve numerical stability. 1.0e-6

Note: The resultant projection matrix P satisfies: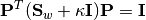

$\mathbf{P}^T (\mathbf{S}_w + \kappa \mathbf{I}) \mathbf{P} = \mathbf{I}$

Here, $\kappa$ equals regcoef * eigmax(Sw). The columns of P are arranged in descending order of the corresponding generalized eigenvalues.

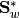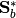Note that MulticlassLDA does not currently support the normalized version using $\mathbf{S}_w^*$ and $\mathbf{S}_b^*$ (see SubspaceLDA below).

Task Functions¶

The multi-class LDA consists of several steps:

Compute statistics, such as class means, scatter matrices, etc.
Solve the projection matrix.
Construct the model.

Sometimes, it is useful to only perform one of these tasks. The package exposes several functions for this purpose:

multiclass_lda_stats(nc, X, y)¶

Compute statistics required to train a multi-class LDA.

Parameters:	nc – the number of classes X – the matrix of input samples. y – the vector of class labels.

This function returns an instance of MulticlassLDAStats, defined as below, that captures all relevant statistics.

type MulticlassLDAStats
    dim::Int                    # sample dimensions
    nclasses::Int               # number of classes
    cweights::Vector{Float64}   # class weights
    tweight::Float64            # total sample weight
    mean::Vector{Float64}       # overall sample mean
    cmeans::Matrix{Float64}     # class-specific means
    Sw::Matrix{Float64}         # within-class scatter matrix
    Sb::Matrix{Float64}         # between-class scatter matrix
end

This type has the following constructor. Under certain circumstances, one might collect statistics in other ways and want to directly construct this instance.

MulticlassLDAStats(cweights, mean, cmeans, Sw, Sb)¶

Construct an instance of type MulticlassLDAStats.

Parameters:	cweights – the class weights, a vector of length `m`. mean – the overall sample mean, a vector of length `d`. cmeans – the class-specific sample means, a matrix of size `(d, m)`. Sw – the within-class scatter matrix, a matrix of size `(d, d)`. Sb – the between-class scatter matrix, a matrix of size `(d, d)`.

multiclass_lda(S; ...)¶

Perform multi-class LDA based on given statistics. Here S is an instance of MulticlassLDAStats.

This function accepts the following keyword arguments (as above): method, outdim, and regcoef.

mclda_solve(Sb, Sw, method, p, regcoef)¶

Solve the projection matrix given both scatter matrices.

Parameters:	Sb – the between-class scatter matrix. Sw – the within-class scatter matrix. method – the choice of method, which can be either `:gevd` or `:whiten`. p – output dimension. regcoef – regularization coefficient.

mclda_solve!(Sb, Sw, method, p, regcoef)

Solve the projection matrix given both scatter matrices.

Note: In this function, Sb and Sw will be overwritten (saving some space).

Subspace LDA¶

The package also defines a SubspaceLDA type to represent a multi-class LDA model for high-dimensional spaces. MulticlassLDA, because it stores the scatter matrices, is not well-suited for high-dimensional data. For example, if you are performing LDA on images, and each image has 10^6 pixels, then the scatter matrices would contain 10^12 elements, far too many to store directly. SubspaceLDA calculates the projection direction without the intermediary of the scatter matrices, by focusing on the subspace that lies within the span of the within-class scatter. This also serves to regularize the computation.

immutable SubspaceLDA{T<:Real}
    projw::Matrix{T}   # P, project down to the subspace spanned by within-class scatter
    projLDA::Matrix{T} # L, LDA directions in the projected subspace
    λ::Vector{T}
    cmeans::Matrix{T}
    cweights::Vector{Int}
end

This supports all the same methods as MulticlassLDA, with the exception of the functions that return a scatter matrix. The overall projection is represented as a factorization P*L, where P'*x projects data points to the subspace spanned by the within-class scatter, and L is the LDA projection in the subspace. The projection directions w (the columns of projection(M)) satisfy the equation

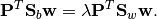
$\mathbf{P}^T \mathbf{S}_b \mathbf{w} = \lambda \mathbf{P}^T \mathbf{S}_w \mathbf{w}.$

When P is of full rank (e.g., if there are more data points than dimensions), then this equation guarantees that Eq. (1) will also hold.

SubspaceLDA also supports the normalized version of LDA via the normalize keyword:

M = fit(SubspaceLDA, X, label; normalize=true)

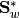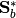would perform LDA using the equivalent of $\mathbf{S}_w^*$ and $\mathbf{S}_b^*$ .