Factor Analysis¶
Factor Analysis (FA) is a linear-Gaussian latent variable model that is closely related to probabilistic PCA. In contrast to the probabilistic PCA model, the covariance of conditional distribution of the observed variable given the latent variable is diagonal rather than isotropic [BSHP06].
This package defines a FactorAnalysis type to represent a factor analysis model, and provides a set of methods to access the properties.
Properties¶
Let M be an instance of FactorAnalysis, d be the dimension of observations, and p be the output dimension (i.e the dimension of the principal subspace)
-
indim(M)¶ Get the input dimension
d, i.e the dimension of the observation space.
-
outdim(M)¶ Get the output dimension
p, i.e the dimension of the principal subspace.
-
mean(M)¶ Get the mean vector (of length
d).
-
projection(M)¶ Get the projection matrix (of size
(d, p)). Each column of the projection matrix corresponds to a principal component.The principal components are arranged in descending order of the corresponding variances.
-
loadings(M)¶ The factor loadings matrix (of size
(d, p)).
-
cov(M)¶ The diagonal covariance matrix.
Transformation and Construction¶
Given a probabilistic PCA model M, one can use it to transform observations into latent variables, as
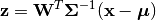
or use it to reconstruct (approximately) the observations from latent variables, as
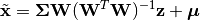
Here, 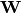 is the factor loadings or weight matrix,
is the factor loadings or weight matrix, 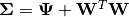 is the covariance matrix.
is the covariance matrix.
The package provides methods to do so:
-
transform(M, x)¶ Transform observations
xinto latent variables.Here,
xcan be either a vector of lengthdor a matrix where each column is an observation.
-
reconstruct(M, z)¶ Approximately reconstruct observations from the latent variable given in
z.Here,
ycan be either a vector of lengthpor a matrix where each column gives the latent variables for an observation.
Data Analysis¶
One can use the fit method to perform factor analysis over a given dataset.
-
fit(FactorAnalysis, X; ...)¶ Perform factor analysis over the data given in a matrix
X. Each column ofXis an observation.This method returns an instance of
FactorAnalysis.Keyword arguments:
Let
(d, n) = size(X)be respectively the input dimension and the number of observations:name description default method The choice of methods:
:em: use EM version of factor analysis:cm: use CM version of factor analysis
:cmmaxoutdim Maximum output dimension d-1mean The mean vector, which can be either of:
0: the input data has already been centralizednothing: this function will compute the mean- a pre-computed mean vector
nothingtol Convergence tolerance 1.0e-6tot Maximum number of iterations 1000η Variance low bound 1.0e-6Notes:
- This function calls
facmorfaeminternally, depending on the choice of method.
Example:
using MultivariateStats
# suppose Xtr and Xte are training and testing data matrix,
# with each observation in a column
# train a FactorAnalysis model
M = fit(FactorAnalysis, Xtr; maxoutdim=100)
# apply FactorAnalysis model to testing set
Yte = transform(M, Xte)
# reconstruct testing observations (approximately)
Xr = reconstruct(M, Yte)
Core Algorithms¶
Two algorithms are implemented in this package: faem and facm.
-
faem(S, mean, n; ...)¶ Perform factor analysis using an expectation-maximization algorithm for a given sample covariance matrix
S[RUBN82].Parameters: - S – The sample covariance matrix.
- mean – The mean vector of original samples, which can be a vector of length
d, or an empty vectorFloat64[]indicating a zero mean. - n – The number of observations.
Returns: The resultant FactorAnalysis model.
Note: This function accepts two keyword arguments:
maxoutdim,``tol``, andtot.
-
facm(S, mean, n; ...)¶ Perform factor analysis using an fast conditional maximization algorithm for a given sample covariance matrix
S[ZHAO08].Parameters: - S – The sample covariance matrix.
- mean – The mean vector of original samples, which can be a vector of length
d, or an empty vectorFloat64[]indicating a zero mean. - n – The number of observations.
Returns: The resultant FactorAnalysis model.
Note: This function accepts two keyword arguments:
maxoutdim,tol,tot, andη.