Canonical Correlation Analysis¶

Canonical Correlation Analysis (CCA) is a statistical analysis technique to identify correlations between two sets of variables. Given two vector variables X and Y, it finds two projections, one for each, to transform them to a common space with maximum correlations.

The package defines a CCA type to represent a CCA model, and provides a set of methods to access the properties.

Properties¶

Let M be an instance of CCA, dx be the dimension of X, dy the dimension of Y, and p the output dimension (i.e the dimensio of the common space).

xindim(M)¶: Get the dimension of X, the first set of variables.

yindim(M)¶: Get the dimension of Y, the second set of variables.

outdim(M)¶: Get the output dimension, i.e that of the common space.

xmean(M)¶: Get the mean vector of X (of length dx).

ymean(M)¶: Get the mean vector of Y (of length dy).

xprojection(M)¶: Get the projection matrix for X (of size (dx, p)).

yprojection(M)¶: Get the projection matrix for Y (of size (dy, p)).

correlations(M)¶: The correlations of the projected componnents (a vector of length p).

Transformation¶

Given a CCA model, one can transform observations into both spaces into a common space, as

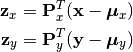
$\mathbf{z}_x = \mathbf{P}_x^T (\mathbf{x} - \boldsymbol{\mu}_x) \\ \mathbf{z}_y = \mathbf{P}_y^T (\mathbf{y} - \boldsymbol{\mu}_y)$

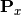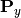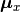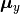Here, $\mathbf{P}_x$ and $\mathbf{P}_y$ are projection matrices for X and Y; $\boldsymbol{\mu}_x$ and $\boldsymbol{\mu}_y$ are mean vectors.

This package provides methods to do so:

xtransform(M, x)¶

Transform observations in the X-space to the common space.

Here, x can be either a vector of length dx or a matrix where each column is an observation.

ytransform(M, y)¶

Transform observations in the Y-space to the common space.

Here, y can be either a vector of length dy or a matrix where each column is an observation.

Data Analysis¶

One can use the fit method to perform CCA over given datasets.

fit(CCA, X, Y; ...)¶

Perform CCA over the data given in matrices X and Y. Each column of X and Y is an observation.

X and Y should have the same number of columns (denoted by n below).

This method returns an instance of CCA.

Keyword arguments:

name description default

method

The choice of methods:

:cov: based on covariance matrices
:svd: based on SVD of the input data

:svd

outdim The output dimension, i.e dimension of the common space min(dx, dy, n)

mean

The mean vector, which can be either of:

0: the input data has already been centralized
nothing: this function will compute the mean
a pre-computed mean vector

nothing

Notes: This function calls ccacov or ccasvd internally, depending on the choice of method.

Core Algorithms¶

Two algorithms are implemented in this package: ccacov and ccasvd.

ccacov(Cxx, Cyy, Cxy, xmean, ymean, p)¶

Compute CCA based on analysis of the given covariance matrices, using generalized eigenvalue decomposition.

Parameters:

Cxx – The covariance matrix of X.
Cyy – The covariance matrix of Y.
Cxy – The covariance matrix between X and Y.
xmean – The mean vector of the original samples of X, which can be a vector of length dx, or an empty vector Float64[] indicating a zero mean.
ymean – The mean vector of the original samples of Y, which can be a vector of length dy, or an empty vector Float64[] indicating a zero mean.
p – The output dimension, i.e the dimension of the common space.

Returns:

The resultant CCA model.

ccasvd(Zx, Zy, xmean, ymean, p)¶

Compute CCA based on singular value decomposition of centralized sample matrices Zx and Zy.

Parameters:

Zx – The centralized sample matrix for X.
Zy – The centralized sample matrix for Y.
xmean – The mean vector of the original samples of X, which can be a vector of length dx, or an empty vector Float64[] indicating a zero mean.
ymean – The mean vector of the original samples of Y, which can be a vector of length dy, or an empty vector Float64[] indicating a zero mean.
p – The output dimension, i.e the dimension of the common space.

Returns:

The resultant CCA model.