Classical Multidimensional Scaling¶

In general, Multidimensional Scaling (MDS) refers to techniques that transforms samples into lower dimensional space while preserving the inter-sample distances as well as possible.

Overview of Classical MDS¶

Classical MDS is a specific technique in this family that accomplishes the embedding in two steps:

Convert the distance matrix to a Gram matrix.

This conversion is based on the following relations between a distance matrix D and a Gram matrix G: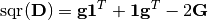

$\mathrm{sqr}(\mathbf{D}) = \mathbf{g} \mathbf{1}^T + \mathbf{1} \mathbf{g}^T - 2 \mathbf{G}$

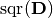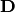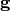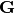Here, $\mathrm{sqr}(\mathbf{D})$ indicates the element-wise square of $\mathbf{D}$ , and $\mathbf{g}$ is the diagonal elements of $\mathbf{G}$ . This relation is itself based on the following decomposition of squared Euclidean distance:

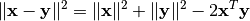
$\| \mathbf{x} - \mathbf{y} \|^2 = \| \mathbf{x} \|^2 + \| \mathbf{y} \|^2 - 2 \mathbf{x}^T \mathbf{y}$
Perform eigenvalue decomposition of the Gram matrix to derive the coordinates.

Functions¶

This package provides functions related to classical MDS.

gram2dmat(G)¶: Convert a Gram matrix G to a distance matrix.

gram2dmat!(D, G): Convert a Gram matrix G to a distance matrix, and write the results to D.

dmat2gram(D)¶: Convert a distance matrix D to a Gram matrix.

dmat2gram!(G, D): Convert a distance matrix D to a Gram matrix, and write the results to G.

classical_mds(D, p[, dowarn=true])¶

Perform classical MDS. This function derives a p-dimensional embedding based on a given distance matrix D.

It returns a coordinate matrix of size (p, n), where each column is the coordinates for an observation.

Note

The Gramian derived from D may have nonpositive or degenerate eigenvalues. The subspace of nonpositive eigenvalues is projected out of the MDS solution so that the strain function is minimized in a least-squares sense. If the smallest remaining eigenvalue that is used for the MDS is degenerate, then the solution is not unique, as any linear combination of degenerate eigenvectors will also yield a MDS solution with the same strain value. By default, warnings are emitted if either situation is detected, which can be suppressed with dowarn=false.

If the MDS uses an eigenspace of dimension m less than p, then the MDS coordinates will be padded with p-m zeros each.

Reference:

@inbook{Borg2005,
Author = {Ingwer Borg and Patrick J. F. Groenen},
Title = {Modern Multidimensional Scaling: Theory and Applications},
Edition = {2},
Year = {2005},
Chapter = {12},
Doi = {10.1007/0-387-28981-X},
Pages = {201--268},
Series = {Springer Series in Statistics},
Publisher = {Springer},
}