Probabilistic Principal Component Analysis¶
Probabilistic Principal Component Analysis (PPCA) represents a constrained form of the Gaussian distribution in which the number of free parameters can be restricted while still allowing the model to capture the dominant correlations in a data set. It is expressed as the maximum likelihood solution of a probabilistic latent variable model [BSHP06].
This package defines a PPCA type to represent a probabilistic PCA model, and provides a set of methods to access the properties.
Properties¶
Let M be an instance of PPCA, d be the dimension of observations, and p be the output dimension (i.e the dimension of the principal subspace)
-
indim(M)¶ Get the input dimension
d, i.e the dimension of the observation space.
-
outdim(M)¶ Get the output dimension
p, i.e the dimension of the principal subspace.
-
mean(M)¶ Get the mean vector (of length
d).
-
projection(M)¶ Get the projection matrix (of size
(d, p)). Each column of the projection matrix corresponds to a principal component.The principal components are arranged in descending order of the corresponding variances.
-
loadings(M)¶ The factor loadings matrix (of size
(d, p)).
-
var(M)¶ The total residual variance.
Transformation and Construction¶
Given a probabilistic PCA model M, one can use it to transform observations into latent variables, as
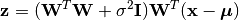
or use it to reconstruct (approximately) the observations from latent variables, as
![\tilde{\mathbf{x}} = \mathbf{W} \mathbb{E}[\mathbf{z}] + \boldsymbol{\mu}](_images/math/0f765e1371dc1193b39d268011d7d66cc77cf3ae.png)
Here, 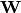 is the factor loadings or weight matrix.
is the factor loadings or weight matrix.
The package provides methods to do so:
-
transform(M, x)¶ Transform observations
xinto latent variables.Here,
xcan be either a vector of lengthdor a matrix where each column is an observation.
-
reconstruct(M, z)¶ Approximately reconstruct observations from the latent variable given in
z.Here,
ycan be either a vector of lengthpor a matrix where each column gives the latent variables for an observation.
Data Analysis¶
One can use the fit method to perform PCA over a given dataset.
-
fit(PPCA, X; ...)¶ Perform probabilistic PCA over the data given in a matrix
X. Each column ofXis an observation.This method returns an instance of
PCA.Keyword arguments:
Let
(d, n) = size(X)be respectively the input dimension and the number of observations:name description default method The choice of methods:
:ml: use maximum likelihood version of probabilistic PCA:em: use EM version of probabilistic PCA:bayes: use Bayesian PCA
:mlmaxoutdim Maximum output dimension. d-1mean The mean vector, which can be either of:
0: the input data has already been centralizednothing: this function will compute the mean- a pre-computed mean vector
nothingtol Convergence tolerance 1.0e-6tot Maximum number of iterations 1000Notes:
- This function calls
ppcaml,ppcaemorbayespcainternally, depending on the choice of method.
Example:
using MultivariateStats
# suppose Xtr and Xte are training and testing data matrix,
# with each observation in a column
# train a PCA model
M = fit(PPCA, Xtr; maxoutdim=100)
# apply PCA model to testing set
Yte = transform(M, Xte)
# reconstruct testing observations (approximately)
Xr = reconstruct(M, Yte)
Core Algorithms¶
Three algorithms are implemented in this package: ppcaml, ppcaem, and bayespca.
-
ppcaml(Z, mean, tw; ...)¶ Compute probabilistic PCA using on maximum likelihood formulation for a centralized sample matrix
Z.Parameters: - Z – provides centralized samples.
- mean – The mean vector of the original samples, which can be a vector of length
d, or an empty vectorFloat64[]indicating a zero mean.
Returns: The resultant PPCA model.
Note: This function accepts two keyword arguments:
maxoutdimandtol.
-
ppcaem(S, mean, n; ...)¶ Compute probabilistic PCA based on expectation-maximization algorithm for a given sample covariance matrix
S.Parameters: - S – The sample covariance matrix.
- mean – The mean vector of original samples, which can be a vector of length
d, or an empty vectorFloat64[]indicating a zero mean. - n – The number of observations.
Returns: The resultant PPCA model.
Note: This function accepts two keyword arguments:
maxoutdim,tol, andtot.
-
bayespca(S, mean, n; ...)¶ Compute probabilistic PCA based on Bayesian algorithm for a given sample covariance matrix
S.Parameters: - S – The sample covariance matrix.
- mean – The mean vector of original samples, which can be a vector of length
d, or an empty vectorFloat64[]indicating a zero mean. - n – The number of observations.
Returns: The resultant PPCA model.
Note: This function accepts two keyword arguments:
maxoutdim,tol, andtot.Additional notes:
- Function uses the
maxoutdimparameter as an upper boundary when it automatically determines the latent space dimensionality.